4.8 Google招聘筆試
google2013校園招聘筆試題
1、 單項選擇題
1.1如果把傳輸速率定義為單位時間內傳送的信息量(以字節計算)多少。關于一下幾種典型的數據傳輸速率:
1.使用USB2.0閃存盤,往USB閃存盤上拷貝文件的數據傳輸速率
2.使用100M以太網,在局域網內拷貝大文件時網絡上的數據傳輸速率
3.使用一輛卡車拉1000塊單塊1TB裝滿數據的硬盤,以100km/h的速度從上海到天津(100km)一趟所等價的數據傳輸寬帶
4.使用電腦播放MP3,電腦的pci總線到聲卡的數據傳輸速率
在通常情況下,關于這幾個傳輸速率的排序正確的是:
A. 4<1<2<3
B. 1<4<2<3
C.4<1<3<2
D.1<4<3<2
1.2.#define SUB(x,y) x-y
#define ACCESS_BEFORE(element,offset,value) *SUB(&element, offset) =value
int main(){
int array[10]= {1,2,3,4,5,6,7,8,9,10};
int i;
ACCESS_BEFORE(array[5], 4, 6);
printf("array: ");
for (i=0; i<10; ++i){
printf("%d", array);
}
printf("\n");
return (0);
}
A.array: 1 6 3 4 5 6 7 8 9 10
B.array: 6 2 3 4 5 6 7 8 9 10
C.程序可以正確編譯連接,但是運行時會崩潰
D.程序語法錯誤,編譯不成功
1.3 在區間[-2, 2]里任取兩個實數,它們的和>1的概率是:
A.3/8
B.3/16
C.9/32
D.9/64
1.4 小組賽,每個小組有5支隊伍,互相之間打單循環賽,勝一場3分,平一場1分,輸一場不得分,小組前三名出線平分抽簽。問一個隊最少拿幾分就有理論上的出線希望:
A.1
B.2
C.3
D.4
1.5用二進制來編碼字符串“abcdabaa”,需要能夠根據編碼,解碼回原來的字符串,最少需要多長的二進制字符串?
A.12
B.14
C.18
D.24
1.6 10個相同的糖果,分給三個人,每個人至少要得一個。有多少種不同分法
A.33 B.34C.35D.36
1.7 下列程序段,循環體執行次數是:
y=2
while(y<=8)
y=y+y;
A.2
B.16
C.4
D.3
1.8下面哪種機制可以用來進行進程間通信?
A.Socket B.PIPEC.SHARED MEMORYD.以上皆可
1.9 下列關于編程優化的說法正確的是:
A. 使用編譯器的優化選項后程序性能一定會獲得提高
B. 循環展開得越多越徹底,程序的性能越好
C. 寄存器分配能夠解決程序中的數據依賴問題
D. 現代主流C/C++編譯器可以對簡單的小函數進行自動Iinline
1.10 一下程序是用來計算兩個非負數之間的最大公約數:
long long gcd(long long x, long long y){
if( y==0) return 0;
else return gcd (y, x%y);
}
我們假設x,y中最大的那個數的長度為n,基本運算時間復雜度為O(1),那么該程序的時間復雜度為:
A.O(1)
B.O(logn)
C.O(n)
D.O(n^2)
2 程序設計與算法(2.1,2.2為編程題,2.3為算法設計題,只需設計思路和關鍵步驟偽代碼)
2.1 寫函數,輸出前n個素數。函數原型:void print_prime(int N); 不需要考慮整數溢出問題,也不許使用大數處理算法。
2.2 長度為n的數組亂序存放著0至n-1. 現在只能進行0與其他書的swap,請設計并實現排序( 必須采用交換實現)。
2.3 給定一個原串和目標串,能對原串進行如下操作:
1 在給定位置插入一個字符
2 替換任意字符
3 刪除任意字符
要求寫一個程序,返回最少的操作數,使得原串進行這些操作后等于目標串。原串和目標串長度都小于2000.
總結的參考答案:
1.1 A
USB 2.0的理論傳輸極限是480Mbps,但是按照這個速率就沒有選項可選了-.-,所以猜測應該認為是普通U盤寫數據的6MB/s,即48Mbps;
100M以太網的速率就是100Mbps;
卡車拉硬盤,1000x1000x8/3600=2222Mbps,這個應該是最快的;
MP3在256kbps碼率下也平均只有1分鐘2MB,所以不會超過0.3Mbps,所以一定是最慢的。
1.2 D
這道題大家走出考場后爭議非常大。咱啥也不說,直接進mingw跑一下gcc:
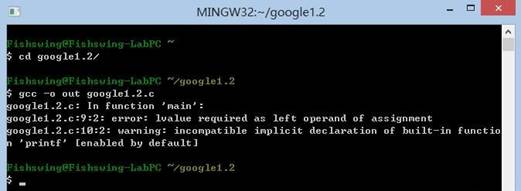
gcc提示的錯誤是“賦值號的左邊操作數需要一個左值”。其原因是調用宏的那句被預處理器替換成了:
*&array-4 =6;
由于減號比賦值優先級高,因此先處理減號;由于減號返回一個數而不是合法的左值,所以編譯報錯。
1.3 C
這道題我是蒙對的-.- 標準做法是先畫出y=1-x的線,上側陰影部分就是y>1-x,其所占比例為9/32:
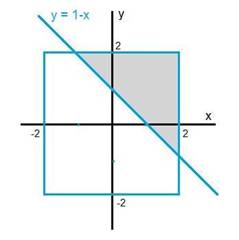
1.4 B
這道題我從A開始湊勝負表,直到B湊出結果就OK了。
1.5 B
這道題需要對abcd進行Huffman編碼。首先根據權值建立Huffman樹,得到最優編碼:
a=0, b=10, c=110, d=111
然后數一下就行了。
1.6 D
這道題我是窮舉的orz……一共這么幾種情況:
118,127,136,145;
226,235,244;
334;
然后有數字重復的算3種排列,不重復的算6種排列,共計4×3+4×6=36種。
1.7 D
這題很基本了。
1.8 D
一般學過操作系統這門課的都會吧,而且個人覺得D這個選項的出現不符合Google風格。
1.9 D
這題其實很好做,因為D肯定是對的,而且ABC的言論太絕對。但如果一定要給出解釋的話……
A選項的優化只能針對代碼本身,純系統調用什么的是不會性能提升的(當然也不會下降),
B選項我覺得是在并行優化方面,好的編譯器可以從循環中發掘并行性,展開之后就不行了,
C選項有點說不清。消除數據依賴主要有兩個方法,一種是SSA,即靜態單賦值,這是通過對變量進行重命名實現的,嚴格的說應該叫“寄存器重命名”而不是“寄存器分配”;另外一種是調換指令順序,這種只要不是真相關(寫后讀,RAW)的話都可以消除掉,也不屬于寄存器分配。所以感覺不應該選這個。
1.10 B
求最大公約數用的是輾轉相除法(歐幾里得算法),所以是O(logn)。
2.1
這題比較基本,而且很多企業的筆試都愛考類似的。主要就是對嘗試對數a進行質因數分解,最容易寫的就是從2開始一直除到sqrt(a),性能提升一點就從2,3然后除奇數一直到sqrt(a)。當然還可以優化一下,建立一個動態質數鏈表,將之前取到的所有質數加入表進行加速。
2.2
這題我覺得除了重載一下swap函數然后用傳統排序法之外也想不出什么高效的做法了。而且要代碼實現,時間緊迫也不由得你多想。
2.3
這題個人覺得是這場筆試唯一拉分的題了,基于動態規劃算法。事實上就是寫出LD算法的偽代碼。
寫出這樣一個函數 ,輸入一個 n, 輸出從1到這個數字之間的出現的1的個數,比如f(13)等于6; f(9)等于1; 網上有很多這道題的解法,大多采用窮舉法。這把這個算法題變成了程序設計,這道題,我認為是總結一個遞推公式,然后用遞推法實現,比較好。后來在網上考證了一下,這道題本來也是讓總結一個數學函數即可,無需編程。既然寫了,就貼出來,發表一下自己的解法。這道題還有另一半,當f(n)=n是,最小的n是多少?本人還沒有好的方法,所以就不貼了。
下面的程序是上半部java實現的。
/* 可以推出下列遞推公式:
* f(n)=(a>1?s:n-s*a+1)+a*f(s-1)+f(n-s*a)當n>9時;
* L是n的位數
* a是n的第一位數字
* s是10的L-1次方
* n-s*a求的是a后面的數.
* 公式說明:
* 求 0-n 由多少個數字1,分三部分,一是所有數中第一位有多少個1,對應(a>1?s:n-s*a+1)
* 當a大于1是,應該有a的L1次, a小于1是有n-s*a+1。
* 如n是223 所有數中第一位有1是100;n是123所有數中第一位是1的有24
* 二是 對應a*f(s-1) 如n是223應該有2*f(99)個1
* 三是 對應f(n-s*a) 如n是223應該有f(23)個1。
*/
long f(long n){
if (n<9) return n>0?1:0;
int L=(int)(Math.log10(n)+1);//求n的位數l
long s=(long)Math.pow(10, L-1);//求10的l-1次方,方便求后面n的第一位數字,及其后面的數。
long a=(long)(n/s);//求n的第一位數字
return (a>1?s:n-s*a+1)+a*f(s-1)+f(n-s*a);
}
google筆試題:A+B=C
在一個集合S中尋找最大的C使A+B=C且A,B,C均在集合當中
解答(原創)
1,將集合S中的數排序X1<=X2<=X3.............Xn;
2,for(i=n;i>0;i--)
{
for(j=0,k=i-1;k>j;)
{
if(Xj+Xk>Xi)
{
k--;
cotinue;
}
if(Xj+Xk<Xi)
{
j++;
contiue;
}
A=Xj;
B=Xk;
C=Xi;
break;
}
例子:
1,4,7,10,11,13,15,18,34
34:1-18,4-18........15-18
18:1-15,4-15,4-13,7-13,7-11
結果:
A=7;B=11,C=18;
第一個的題目(嗯,記的不是很完整):
在一棵(排序?)二叉樹中搜索指定值,數據結構定義為:
struct Node
{
Node * lnext;
Node * rnext;
int value;
};
函數定義為():
Node * search(Node * root, int value)
{
}
實現這個search函數。
用遞歸,經典的樹的遍歷,pass先。
第二個的題目:
計算Tribonaci隊列(嗯,九成九記錯了那個單詞……),規則是T(n) = T(n - 1) T(n - 2) T(n -3),其中T(0) = T(1) = 1,T(2) = 2。
函數定義:
int Tribonaci(int n) {
}
備注,不考慮證整數溢出,盡可能優化算法。
這一題我一看就知道要考什么,很顯然的遞歸定義,但也是很顯然的,這里所謂的優化是指不要重復計算。
簡單的說,在計算T(n)的時候要用到T(n - 1)、T(n - 2)和T(n - 3)的結果,在計算T(n - 1)的時候也要用到T(n - 2)和T(n - 3)的結果,所以在各項計算的時候必須把以前計算的結果記錄下來,去掉重復計算。這里用到的一點小技巧就是要新寫一個函數用來做這種事情,嗯,看看我寫的代碼吧!
/**
Get the value of T(n - 1), and retrieve the result of
T(n - 2) and T(n - 3).
@param[in] n The n in T(n).
@param[out] mid Value of T(n - 2).
@param[out] right Value of T(n - 3).
@return Value of T(n - 1).
*/
int find_trib(int n, int & mid, int & right)
{
if (3 == n)
{
mid = 1;
right = 1;
return 2;
}
else
{
int temp;
mid = find_trib(n - 1, right, temp);
return mid right temp;
}
}
/**
Find value of T(n).
@param[in] The n in T(n).
@return Value of T(n).
@note T(n) = T(n - 1) T(n - 2) T(n - 3) (n > 2)
T(0) = T(1) = 1, T(2) = 2.
*/
int tribonaci(int n)
{
if (n < 0)
{
// Undefined feature.
return 0;
}
if (0 == n || 1 == n)
{
return 1;
}
if (2 == n)
{
return 2;
}
int mid, right;
int left = find_trib(n, mid, right);
return left mid right;
}
啊啊,對了,答卷的時候我可沒心情寫注釋……剛才到VC.Net 2003上測試了一下,貌似沒有啥問題。唉,看來我多少還是懂一點算法的……
第三個的題目:
05年Google筆試題
要筆試考題如下,其他題目是基礎題,就不貼出了:
1、假設在n進制下,下面的等式成立,n值是()
567*456=150216
a、 9 b、 10 c、 12 d、 18
2、文法G:S->uvSvu|w所識別的語言是:()
a、uvw*vu b、(uvwvu)* c、uv(uv)*wvu(vu)* d、(uv)*w(vu)*
3、如下程序段輸出是:()
char str[][10]={"Hello","Google"};
char *p=str[0];
count<<strlen(p 10);
a、0 b、5 c、6 d、10
4、cnt=0
while(x!=1){
cnt=cnt 1;
if(x&1==0)
x=x/2;
else
x=3*x 1;
}
count<<cnt<<end1;
當n=11時,輸出:()
a、12 b、13 c、14 d、15
5、寫一段程序判定一個有向圖G中節點w是否從節點v可達。(假如G中存在一條從v至w的路徑就說節點w是從v可達的)。以下算法是用C 寫成的,在bool Reachable函數中,你可以寫出自己的算法。
class Graph{
public:
int NumberOfNodes();//返回節點的總數
bool HasEdge(int u,int v);//u,v是節點個數,從零開始依次遞增,當有一條從u到v的邊時,返回true
};
bool Reachable(Graph&G, int v, int w){
//請寫入你的算法
}
6、給定一棵所有邊的長度均為整數的樹,現要求延長其中某些邊,使得從根到任意節點的路徑長度相等。問滿足要求的樹的邊長度之和最小是多少?請寫出你的算法,并分析時間復雜度。
=====================================================================
Google筆試題
1、 兩個二進制數的異或結果
2、 遞歸函數最終會結束,那么這個函數一定(不定項選擇):
1. 使用了局部變量 2. 有一個分支不調用自身
3. 使用了全局變量或者使用了一個或多個參數
3、以下函數的結果?
int cal(int x)
{
if(x==0)
return 0;
else
return x+cal(x-1);
}
4、 以下程序的結果?
void foo(int*a, int* b)
{
*a = *a+*b;
*b = *a-*b;
*a = *a-*b;
}
void main()
{
int a=1, b=2, c=3;
foo(&a,&b);
foo(&b,&c);
foo(&c,&a);
printf("%d, %d, %d", a,b,c);
}
5、下面哪項不是鏈表優于數組的特點?
1. 方便刪除 2. 方便插入 3. 長度可變 4. 存儲空間小
6、T(n) = 25T(n/5)+n^2的時間復雜度?
7、n個頂點,m條邊的全連通圖,至少去掉幾條邊才能構成一棵樹?
8、正則表達式(01|10|1001|0110)*與下列哪個表達式一樣?
1.(0|1)* 2.(01|01)* 3.(01|10)* 4.(11|01)* 5.(01|1)*
9、如何減少換頁錯誤?
1. 進程傾向于占用CPU 2. 訪問局部性(locality of reference)滿足進程要求
3. 進程傾向于占用I/O 4.使用基于最短剩余時間(shortest remaining time)的調度機制
5. 減少頁大小
10、實現兩個N*N矩陣的乘法,矩陣由一維數組表示
11、找到單向鏈表中間那個元素,如果有兩個則取前面一個
12、長度為n的整數數組,找出其中任意(n-1)個乘積最大的那一組,只能用乘法,不可以用除法。要求對算法的時間復雜度和空間復雜度作出分析,不要求寫程序。
google浙大招聘筆試題
一、單選
1、80x86中,十進制數-3用16位二進制數表示為?0010000
2、假定符號-、*、$分別代表減法、乘法和指數運算,且
1)三個運算符優先級順序是:-最高,*其次,$最低;
2)運算符運算時為左結合。請計算3-2*4$1*2$3的值:
(A)4096,(B)-61,(C)64,(D)-80,(E)512
算符
3、下列偽代碼中,參數是引用傳遞,結果是?
calc(double p, double q, double r){q=q-1.0;r=r+p}
main(){
double a = 2.5, b = 9.0;
calc(b-a, a, a);
print(a);
}
(A)1.5 (B)2.5 (C)10.5 (D)8 (E)6.5
4、求輸出結果:
int foo(int x, int y){
if(x <=0 || y <= 0) return 1;
return 3 * foo(x - 1, y / 2);
}
printf("%d\n", foo(3, 5));
(A)81 (B)27 (C)9 (D)3 (E)1
5、下列哪個數據結構在優先隊列中被最廣泛使用?a
(A)堆 (B)數組 (C)雙向鏈表 (D)圖 (E)向量
6、以下算法描述了一個在n國元素的雙向鏈表中找到第k個元素的方法(k >= 1且k <= n):
如果k <= n - k,從鏈表開始往前進k-1個元素。
否則,從終點出發,往回走n - k個元素。
這個算法的時間代價是?
(A)θ(nlogn) (B)θ(max{k, n - k}) (C)θ(k + (n - k))
(D)θ(max{k, k - n}) (E)θ(min{k, n - k})
7、有一個由10個頂點組成的圖,每個頂點有6個度,那么這個圖有幾條邊?30
(A)60 (B)30 (C)20 (D)80 (E)90
8、正則表達式L = x*(x|yx+)。下列哪個字符串不符號
(A)x (B)xyxyx (C)xyx (D)yxx (E)yx
9、為讀取一塊數據而準備磁盤驅動器的總時間包括
(A)等待時間 (B)尋道時間 (C)傳輸時間 (D)等待時間加尋道時間 (E)等待時間加尋道時間加傳輸時間
二、算法
1、打印出一個二叉樹的內容。
2、在一個字符串中找到第一個只出現一次的字符。如abaccdeff,輸出b。
3、給定一個長度為N的整數數組(元素有正有負),求所有元素之和最大的一個子數組。分析算法時空復雜度。不必寫代碼。
附上算法題第3題的動態規劃做法的參考答案:
最大子序列
問題:
給定一整數序列A1, A2,... An (可能有負數),求A1~An的一個子序列Ai~Aj,使得Ai到Aj的和最大
例如: 整數序列-2, 11, -4, 13, -5, 2, -5, -3, 12, -9的最大子序列的和為20。 對于這個問題,最簡單也是最容易想到的那就是窮舉所有子序列的方法。利用三重循環,依次求出所有子序列的和然后取最大的那個。當然算法復雜度會達到O(n^3)。顯然這種方法不是最優的,下面給出一個算法復雜度為O(n)的線性算法實現,算法的來源于Programming Pearls一書。 在給出線性算法之前,先來看一個對窮舉算法進行優化的算法,它的算法復雜度為O(n^2)。其實這個算法只是對對窮舉算法稍微做了一些修改:其實子序列的和我們并不需要每次都重新計算一遍。假設Sum(i, j)是A[i] ... A[j]的和,那么Sum(i, j+1) = Sum(i, j) + A[j+1]。利用這一個遞推,我們就可以得到下面這個算法:
int max_sub(int a[],int size)
{
int i,j,v,max=a[0];
for(i=0;i<size;i++)
{
v=0;
for(j=i;j<size;j++)
{
v=v+a[j];//Sum(i, j+1) = Sum(i, j) + A[j+1]
if(v>max)
max=v;
}
}
return max;
}那怎樣才能達到線性復雜度呢?這里運用動態規劃的思想。先看一下源代碼實現:
int max_sub2(int a[], int size)
{
int i,max=0,temp_sum=0;
for(i=0;i<size;i++)
{
temp_sum+=a[i];
if(temp_sum>max)
max=temp_sum;
else if(temp_sum<0)
temp_sum=0;
}
return max;
}
在這一遍掃描數組當中,從左到右記錄當前子序列的和temp_sum,若這個和不斷增加,那么最大子序列的和max也不斷增加(不斷更新max)。如果往前掃描中遇到負數,那么當前子序列的和將會減小。此時temp_sum 將會小于max,當然max也就不更新。如果temp_sum降到0時,說明前面已經掃描的那一段就可以拋棄了,這時將temp_sum置為0。然后,temp_sum將從后面開始將這個子段進行分析,若有比當前max大的子段,繼續更新max。這樣一趟掃描結果也就出來了。
google面試試題匯總
筆試題目:9道單選+3道問答
時間:100分鐘
我做的是B卷。
單選題:
1,求兩個二進制數的異或值,基本上學過一點計算機的東西的人都能對的題目。。
2,不記得了。。也是不需要思考的題目。。
3,大概是如下的函數:
int someFunc(int x){
if (x == 0)
return 0;
else
return x + someFunc(x - 1);
}
問這個計算的是什么。。。
4,不記得了。。不需要思考吧。。
5,不記得了。。不需要思考吧。。
6,參見2,4,5。。
7,似乎需要思考一下。。
8,問鏈表結構和數組相比的優勢不包括哪項,
包括:
插入的時間
刪除的時間
存儲空間
剩下兩個不記得了。。
9,如下函數:
T(x) = 1 (x <= 1)
T(n) = 25 T(n/5) + n^2
問T(n)隨n的增長。
選項大概是這樣的:
O(n^2),O(n^2logn)等等的。。
問答:
1,寫兩個N*N的矩陣的乘法,給出了C的格式,你可以選擇你喜歡的語言去寫。。
int* multi(int* a1, int* a2, int N){
}
2,尋找一個單向鏈表的中項,如果存在兩個則返回前一個。給出了C的格式,同樣你可以選擇。。。。
struct {
Node* next;
int value;
} Node;
Node* someFunc(Node* head){
}
3,給一個長度為n的整數數組,只允許用乘法不允許用除法,計算任意(n-1)個數的組合乘積中最大的一組。。。寫出算法的時空復雜度。
ps:懷疑這道題目出錯啦。。雖然我也做錯了。。。。。。
一些補充:
1,問答的第一題是google上學期 intern的大題原題;
2,google很喜歡考鏈表,無論intern的面試以及兩次的筆試都有這樣的題目;
3,google一般大題第三道都是寫算法的時空復雜度;
4,選擇題基本上偏簡單,但是要做得準確率高似乎并不那么容易;
5,根據傳言,小道消息,人云亦云以及以訛傳訛,google的高速審卷政策來源于審卷時以選擇題為主,如果你全對啦,那么恭喜你pass啦;如果你錯了好幾道,那么下次努力吧,如果還有下次。。。大題基本是做參考的。。。
Google筆試題2006
選擇題
1. 把一個無符號16位整數a的最高為置為1
2. Fibonacci,求f(4)使用遞歸調用f(1)的次數f(n) = f(n-1)+f(n-2)
f(0)=0, f(1)=1
a.5 b.4 c. 3 d. 4以上
3. if (xAS{print “1″}
S->AB{print “2″}
A->a{print “3″}
B->bC{print “4″}
B->dB{print “5″}
C->c{print “6″}
6. 有關哈希表正確的說法(不定項)
a.哈希表的效率和哈希函數。。。。相關
b.哈希表的解決沖突方法慢,回影響哈希表效率
c.使用鏈表哈希可使內存緊湊
7. 一種無饑餓調度方法是:
a. 輪叫調度
b.
c. 最短使用時間
d. 最新隊列
8. 下列排序方法最差情況時間復雜度為O(n^2)的是:
a. 插入
b. 歸并
c. 冒泡
d. 快速
編程題:
1. 求一個二叉樹的高度,如果只有root結點,高度為0
2. 將稀疏疏組中的非零元素提取出來,用鏈表表示
3. 兩個n維數組,已排序,為升序。設計算法求2n的數中
第n大的數。要求分析時間和空間復雜度。不用給出代碼
==================================================================
這是部分google面試題目,希望后來者好運.
1.求直方圖的最大內接矩形,假設每個細條的寬度為1.這個題很hot,兩個人來問.我沒想出什么好的算法.
2.NxN行列有序的矩陣查找一個數.以前有人遇到過.O(N)的時間復雜度
3.給定一篇文章,求包含所有單詞的最短摘要.O(N)的時間復雜度
4.將MxN的矩陣轉秩,要求O(1)的空間復雜度.參考群論中cyclic group,group generator
5.開放式問題,怎么避免重復抓取網頁
6.開放式問題,有些網站每天只允許有限次訪問,怎么抓取網頁使得索引盡量全面和新鮮
7.寫一個singleton pattern的例子
8.vector vs. arraylist, growth strategy & complexity
9.在C++文件中只declare class A, 但不以任何方式define class A, 是做什么用
10.virtual function
11.討論html vs. xhtml vs. xml
12.描述在瀏覽器中敲入一個網址后所發生的事情.dns,cache等
